Leonardo Bigollo, meglio conosciuto come Leonardo Fibonacci, era un matematico italiano vissuto oltre 900 anni fa nel 1200d.C.. Fibonacci ci ha fornito il sistema dei numeri decimali (questo è un altro modo per dire i numeri che usiamo in questo momento: 1, 2, 3, 4, 5, 6, 7, 8, 9 e 0).
Prima di lui, molte persone usavano i numeri romani (I, II, III, IV, V, VI, VII, VIII, IX e così via). Ma non è solo quello per cui è famoso. Nel testo in seguito troverai infatti tutto quello che è più interessante sulla vita di Fibonacci, fino alla matematica, tra cui la sequenza e la spirale di Fibonacci, e tutto spiegato semplicemente per i bambini della scuola primaria.
Ti può anche interessare:
In seguito troverai la vita e la matematica di Fibonacci spiegato per bambini della scuola primaria. Fai riferimento all’indice dei contenuti qui sotto per passare velocemente alla parte desiderata.
Indice
- Chi era Leonardo Fibonacci? Biografia e sequenza
- Sequenza di Fibonacci spiegata ai bambini
- Fibonacci spiegato con i conigli
- Cos’è la spirale di Fibonacci?
- Dove troviamo la spirale di Fibonacci?
- Creare il proprio schema di Fibonacci
- Libri consigliati
Chi era Leonardo Fibonacci? Biografia e sequenza
Leonardo Pisano, detto Fibonacci, da filius Bonaccii, perché figlio di Guglielmo Bonacci, è un personaggio di importanza centrale nella matematica e nella cultura di epoca medievale.
Fibonacci nacque in Italia, a Pisa nel 1170, ma venne educato nel Nord Africa, dove, il padre Guglielmo, lavorava come diplomatico.
Suo padre era infatti segretario della Repubblica di Pisa e responsabile del commercio pisano presso la colonia di Bugia, una città in Algeria, dove i Pisani intrattenevano fiorenti traffici commerciali. Trascorse gran parte della giovinezza, al seguito del padre e lo seguì in diversi viaggi.
Suo padre voleva che Leonardo divenisse un mercante e così si assicuro che studiasse le tecniche del calcolo. Fu proprio qui che Fibonacci ebbe modo di apprendere tecniche matematiche ancora del tutto sconosciute in Occidente.

Nel 1200 ritornò a Pisa dove scrisse diversi testi importanti. Tornato in Italia riuscì a risolvere facilmente alcuni problemi che gli aveva posto il re relativo ai conigli, Federico II, il quale restò affascinato dalla mente di Fibonacci e decise di dargli un sostegno economico affinché potesse continuare a studiare la matematica senza dover lavorare.
Dobbiamo ricordare che Fibonacci viveva in un periodo in cui la stampa non era ancora stata inventata, quindi scriveva tutti i suoi libri a mano. Immaginate quindi, quanto tempo e quanto fosse difficile conservare i suoi manoscritti, ne scrisse tanti, ma purtroppo molti testi andarono persi.
Uno di questi manoscritti però è giunto fino a noi, s’intitola “Liber abbaci”, che scrisse a soli 32 anni.
Questo libro contribuì in modo determinante a mostrare i vantaggi dell’uso delle cifre e della numerazione araba nella soluzione di vari problemi di calcolo.
Non solo, oltre ad essere un saggio che rivoluzionerà la numerazione romana, è anche un manuale per commercianti.
Nella prima parte di quest’ opera introdusse in Europa il sistema di cifre decimali indo-arabico e l’uso dei numeri arabi.
Cosa sono i numeri arabi?
A differenza di quello che possiamo immaginare, i numeri arabi sono i numeri che usiamo nella vita quotidiana, 0 1 2 3 4 5 6 7 8 9. Si chiamano così, non perché sono stati inventati dagli arabi, ma perché sono stati introdotti a noi, grazie al lavoro di alcuni astronomi arabi. Tuttavia, il maggiore contributo nella conoscenza di questi numeri è stato dato da Fibonacci, che li introdusse nella cultura occidentale.
Questo sistema numerico però non fu subito ben accettato, addirittura la città di Firenze ne vietò l’uso, perché si pensava che il numero zero creasse confusione.

Il principale vantaggio di queste dieci cifre, appunto i numeri arabi, sta nel fatto che è possibile formare tutti i numeri, a differenza dei numeri romani che non bastavano a rappresentare tutte le cifre. Essi arrivano solo fino al 3999 e per rappresentare i numeri più alti bisognava aggiungere speciali linee verticali e orizzontali, che rendevano i calcoli ancora più complicati.
Inoltre, con i numeri romani non si potevano eseguire le operazioni fondamentali e si doveva usare un abaco e infine, nei numeri romani, non esiste il numero zero.
Torniamo al nostro Fibonacci e al suo libro “Liber abbaci”.
La seconda parte del libro era invece dedicata ai mercanti, qui si insegnava loro come calcolare i prezzi dei prodotti, come convertire il denaro e come calcolare il profitto delle vendite. Facile direte voi! Ma in realtà non lo è affatto, ricordatevi che non c’erano computer e calcolatrici!
E infine nella terza parte del libro spiega quella che è nota come la “sequenza di Fibonacci” nella quale ogni numero è la somma dei due numeri che lo precedono. Questa sequenza si dimostrò estremamente importante ed è presente in molte e differenti aree della matematica e della scienza.
Fibonacci morì a Pisa intorno al 1235, 1240, la data della sua morte non è certa.
Sequenza di Fibonacci spiegata ai bambini
La sequenza (o serie ) di Fibonacci è una successione di numeri in cui ciascun numero è la somma dei due precedenti. I primi due termini della successione sono 0 e 1.
Si procede sommando: 0+1= 1 1+1=2 1+2=3 2+3=5 3+5=8 5+8=13 e così via…
Pertanto, i primi termini della successione risultano:0 1 1 2 3 5 8 13 21 34 55 89
Adesso che conosciamo come funziona la sequenza di Fibonacci cerchiamo di capire come viene usata e perché è così importante.
Fibonacci spiegato con i conigli
Si dice che la famosa domanda che il re Federico II, chiese a Fibonacci fosse:
“Quante coppie di conigli si ottengono in un anno, salvo i casi di morte, supponendo che ogni coppia dia alla luce un’altra coppia ogni mese e che le coppie più giovani siano in grado di riprodursi già al secondo mese di vita?”
Cosa c’entra una sequenza di numeri con i conigli?
Per rispondere a questa domanda dobbiamo prima fare i conti mese per mese:
Gennaio: Si parte da 1 coppia, cioè all’inizio la risposta è 1 coppia.
Febbraio: Abbiamo ancora una sola coppia, perché i conigli sono ancora troppo giovani per riprodursi. Quindi la risposta è ancora 1 coppia
Marzo: Al secondo mese abbiamo 1 coppia più la coppia di figli appena nata, cioè 2 coppie.
Aprile: solo 1 delle 2 coppie può avere figli, e dunque si avranno in tutto 3 coppie.
Maggio: delle 3 coppie esistenti al mese precedente solo 2 possono avere figli, e avremo 5 coppie.
Giugno: Il mese successivo potranno avere figli solo le coppie che erano presenti al mese precedente, cioè 3 coppie, e si avranno dunque in tutto 8 coppie.
A luglio abbiamo un totale di 13 coppie … e cosi via…
La successione di numeri che viene fuori è 1, 1, 2, 3, 5, 8, 13.
… Ma questa sequenza mi ricorda qualcosa! E sì, è proprio la sequenza di Fibonacci!
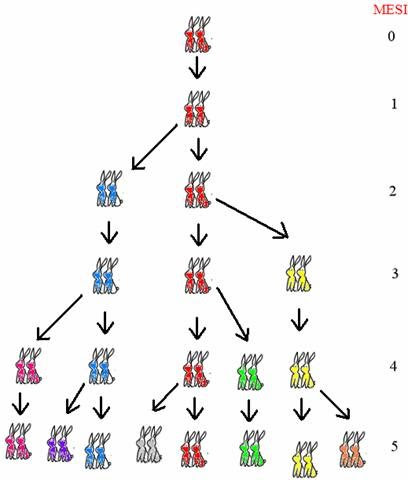
Molti problemi legati allo sviluppo delle popolazioni, umane o animali, sono stati affrontati da un punto di vista matematico con l’aiuto di questa sequenza. Grazie a questa sequenza, Fibonacci, crea la spirale logaritmica comunemente chiamata spirale aurea o spirale di Fibonacci.
Cos’è la spirale di Fibonacci?
Non è facile spiegare a parole come funziona la spirale di Fibonacci, per cui ci aiuteremo con dei disegni che renderanno il tutto più semplice. Potete provarci anche voi!
- Prendiamo un foglio e disegniamo un quadrato. Diciamo che questo quadrato è il numero 1 della sequenza di Fibonacci.
- Ora disegniamo un secondo quadrato attaccato al lato del nostro primo quadrato e lo numeriamo con il secondo numero nella sequenza di Fibonacci, che è sempre 1.
- Il terzo quadrato lo disegniamo utilizzando i lati dei quadrati 1 e 1.
- Nella sequenza di Fibonacci segue il numero 3, quindi il quadrato numero 3 sarà collegato ai lati del quadrato 1 e 2.
- Segue il numero 5, che sarà collegato ai quadrati 1, 1 e 3
- … e cosi’ via, continuiamo fino che il foglio ce lo permette.

A questo punto, partendo dal nostro quadratino iniziale, cominciamo a disegnare una spirale…
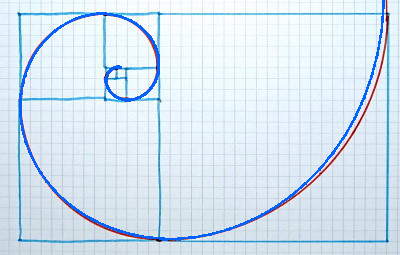
Ecco la spirale di Fibonacci, un cerchio che, invece di chiudersi, continua a girare all’infinito diventando sempre più grande.
Dove troviamo la spirale di Fibonacci?
La spirale di Fibonacci si manifesta spesso nella natura: la ritroviamo nei vortici, nei tifoni, ma anche nella “casa” delle chiocciole o delle conchiglie nella coda dei cavallucci marini, anche i pistilli dei fiori spesso si dispongono a cerchio seguendo la spirale di Fibonacci.

La troviamo anche nella disposizione delle foglie su uno stelo di un albero o nel numero dei petali di un fiore. Per esempio quasi tutti i fiori hanno tre o cinque o otto o tredici o ventuno o trentaquattro petali e così via.
La natura sembra amare la sequenza di Fibonacci! Ma non solo, la troviamo ancora nel corpo umano, nella sezione del dna, in musica, in arte e in architettura!
Creare il proprio schema di Fibonacci
Raccogliete pigne, fiori, sassi, foglie o altro materiale sfuso e provate a disporlo per creare un vostro schema di Fibonacci. Quali materiali si prestano meglio a questo scopo? Dipende dalla forma, dalle dimensioni, dal peso o da un altro fattore?
Pensate a come far seguire a questo esercizio un’attività artistica (in casa o all’aperto) che utilizzi il modello della sequenza di Fibonacci come ispirazione.
Per approfondire puoi guardarti questo brevissimo video che spiega in maniera sintetica la Fibonacci e la sua stupefacente successione.
Libri consigliati
Se volete approfondire vi consiglio di leggere questi libri:
I numeri magici di Fibonacci. L’avventurosa scoperta che cambiò la storia della matematica
Fibonacci, considerato il maggiore matematico del Medioevo, che comprese per primo che le “nove figure indiane” e soprattutto zephirum, lo zero, avrebbero cambiato il mondo in cui viveva? In un affascinante viaggio che ripercorre la vita di questo genio intraprendente, Keith Devlin permette al lettore di riscoprire una figura cruciale e misteriosa del nostro passato, che con le sue ricerche e il suo “Liber abbaci” – il più importante testo di algebra del tempo che spiegava come adottare il sistema numerico indo-arabico – mostrò all’Europa i risvolti pratici e commerciali della matematica, e aprì così la strada all’ascesa del Vecchio continente verso il dominio scientifico ed economico mondiale.
Sezione aurea e successione di Fibonacci
L’autore, nel libro, illustra come la Sezione Aurea sia presente in molte figure geometriche, architetture, ci insegna il metodo, facile ed intuitivo, per individuarla, verificare la sua presenza, che non è mai una semplice presenza, ma la struttura portante dell’opera. Ci guida alla ricerca della Sezione Aurea e della Successione Fibonacci in alcune architetture: il Duomo di Alba, il Duomo di Siena, il Duomo di Firenze.
La sezione aurea. Storia di un numero e di un mistero che dura da tremila anni
In questo libro Mario Livio illustra i miti e la realtà della sezione aurea e mostra il rapporto tra il mondo fisico, le creazioni artistiche e la limpida bellezza dei numeri.




